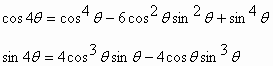الفصل الأول
الأعداد العقدية والتوابع التحليلية
1-1
مقدمةيعرف العدد العقدي(التخيلي) بأنه الزوج المرتب![]() من الأعداد الحقيقية
من الأعداد الحقيقية ![]() ويكتب
بالشكل :
ويكتب
بالشكل : ![]()
يسمى ![]() بالقسم الحقيقي للعدد العقدي
ويرمز له بـ
بالقسم الحقيقي للعدد العقدي
ويرمز له بـ ![]()
ويسمى ![]() بالقسم التخيلي للعدد العقدي
ويرمز له بـ
بالقسم التخيلي للعدد العقدي
ويرمز له بـ ![]()
ويرمز لمجموعة الأعداد العقدية بـ . ![]() حيث أن مجموعة الأعداد الحقيقية
حيث أن مجموعة الأعداد الحقيقية ![]() مجموعة جزئية منها.
مجموعة جزئية منها.
نقول إن العدديين العقديين ![]() أنهما
متساويان إذا كان:
أنهما
متساويان إذا كان:
![]()
جمع العدديين العقديين يعرف بالشكل:
![]()
أما حاصل ضرب العدديين العقديين فيعرف بالشكل:
![]()
أما الشكل الديكارتي للعدد العقدي فهو:
![]()
حيث أن ![]() ، ونلاحظ أن :
، ونلاحظ أن :
![]()
لذلك:
![]()
من الخواص العامة للعدد العقدي نجد أن:
![]()
وبالتالي ![]() وتسمى بوحدة الأعداد
التخيلية.
وتسمى بوحدة الأعداد
التخيلية.
مما سبق يمكن استنتاج علاقة الضرب والقسمة بالشكل الديكارتي:
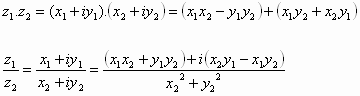
وذلك بضرب البسط والمقام بمرافق المقام.
1-2
المرافق والقيمة المطلقة للعدد العقديمرافق العدد العقدي ![]() هو بالتعريف
هو بالتعريف
![]() ،
،
وبسهولة يمكن استنتاج العلاقات التالية:
![]()
![]()
![]()
![]()
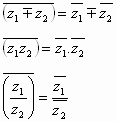
أما القيمة المطلقة (قياس) العدد العقدي والذي يرمز له بالرمز
![]() أو r فهو عدد حقيقي موجب معرف بالعلاقة:
أو r فهو عدد حقيقي موجب معرف بالعلاقة:
![]()
و يمكن الاستنتاج أن:
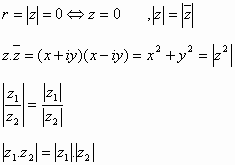
1-3
الشكل القطبي والمعنى الهندسي للعدد العقدي:يتم تعيين النقطة ![]() في المستوي العقدي
بمعرفة قيم
في المستوي العقدي
بمعرفة قيم ![]() أو قيمة الزاوية التي يصنعها الشعاع
أو قيمة الزاوية التي يصنعها الشعاع
![]() مع الاتجاه الموجب للمحور
مع الاتجاه الموجب للمحور ![]() وبالطول
وبالطول ![]() .
.
من الشكل نجد :
![]()
لذلك يمكن كتابة العدد العقدي بالشكل:
![]()
أي أن الأعداد الحقيقة تمثل بنقاط على محور الفواصل بينما الأعداد
العقدية تمثل على محور التراتيب والعدد العقدي يمثل بشعاع بدايته المركز ونهايته
النقطة ![]() وإذا كان
وإذا كان![]() شعاع له نفس
طول واتجاه
شعاع له نفس
طول واتجاه ![]() فان :
فان : ![]()
والأعداد العقدية تجمع وتطرح كما في الأشعة في المستوي
![]() .
.
نسمي الزاوية ![]() بمضمون (عمدة) العدد
العقدي ويرمز لها بالرمز
بمضمون (عمدة) العدد
العقدي ويرمز لها بالرمز ![]() ونسمي
ونسمي
![]() بقياس أو طويلة أو القيمة
المطلقة للعدد العقدي ، ونلاحظ أن:
بقياس أو طويلة أو القيمة
المطلقة للعدد العقدي ، ونلاحظ أن:
![]()
وجميع الزوايا المحققة للعلاقة السابقة هي مضمون العدد العقدي.
نسمي الزاوية في المجال ![]() أو في المجال
أو في المجال
![]() بالتعيين الرئيسي للمضمون، ومن علاقة أولر
بالتعيين الرئيسي للمضمون، ومن علاقة أولر
![]() ، يكتب العدد العقدي بالشكل الأسي:
، يكتب العدد العقدي بالشكل الأسي:
![]()
ويمكن الملاحظة أن :
![]()
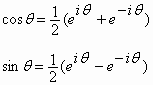
مثال
:أوجد الشكل القطبي للعدد العقدي ![]()
الحل:
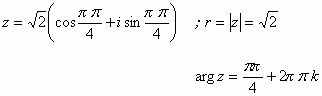
1-4
العمليات الرياضية للأعداد العقدية بالشكل القطبيليكن:
![]()
عندئذٍ:
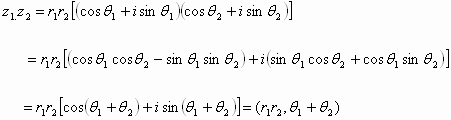
وكذلك :
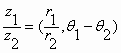
ويمكن استنتاج أن:
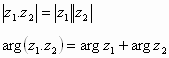
وبشكل مشابه نجد أن:
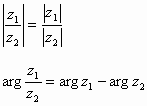
وبصورة عامة فإن:
![]()
وعندما يكون ![]() نجد:
نجد:
![]()
فإذا كانت ![]() عندها نحصل على العلاقة:
عندها نحصل على العلاقة:
![]()
والتي تسمى علاقة دوموافر من أجل جميع قيم
![]() الصحيحة.
الصحيحة.
مثال
: احسبالحل:
حسب دوموافر:
![]()
وحسب دستور نشر ثنائي الحد:
![]()
بالمطابقة نجد: