1-5
جذور الأعداد العقديةإن إيجاد الجذر النوني للعدد العقدي ![]() ،
هو إيجاد عدد عقدي آخر
،
هو إيجاد عدد عقدي آخر ![]() ، بحيث يكون
، بحيث يكون
![]() .
.
أي أن:
![]()
وكذلك: ![]()
ويمكن تمثيل القيم المختلفة برؤوس مضلع منتظم عدد أضلاعه
![]() ونصف قطر الدائرة المارة برؤوسه هو
ونصف قطر الدائرة المارة برؤوسه هو
![]() ومركزها في المبدأ:
ومركزها في المبدأ:
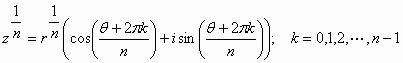
مثال
:احسب جميع قيم ![]()
الحل:
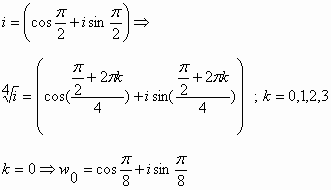
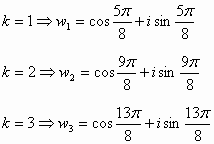
مثال
:احسب قيم الجذر ![]()
الحل:
![]()
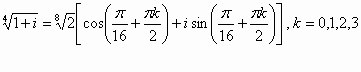
![]()
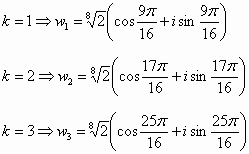
1-6
التوابع العقدية والتحليلية1-6-1
تعاريف- نسمي أي مجموعة من نقاط المستوي العقدي بمجموعة بمجموعة النقاط
![]()
- نسمي مجموعة النقاط الواقعة داخل الدائرة
![]() بالجوار
بالجوار ![]() للنقطة
للنقطة
![]()
(ليس ضرورياً أن يكون الجوار دائرياً) نقول أن
![]() نقطة تراكم (تجمع) للمجموعة
نقطة تراكم (تجمع) للمجموعة ![]() إذا كان أي جوار للنقطة
إذا كان أي جوار للنقطة ![]() يحوي عدد غير منته من نقاط هذه
المجموعة.
يحوي عدد غير منته من نقاط هذه
المجموعة.
- نسمي النقطة ![]() نقطة داخلية للمجموعة
نقطة داخلية للمجموعة
![]() إذا وجد جوار لـ
إذا وجد جوار لـ![]() محتوى بكامله
في
محتوى بكامله
في ![]() نقول إن المجموعة
نقول إن المجموعة ![]() مفتوحة
إذا كانت جميع نقاطها داخلية.
مفتوحة
إذا كانت جميع نقاطها داخلية.
- إذا قابلنا كل عدد طبيعي![]() بعدد عقدي
بعدد عقدي
![]() فان الأعداد :
فان الأعداد :
![]()
تشكل متتالية لانهائية وكل عدد من هذه المتتالية يسمى حداً ونسمي
النقطة ![]() نهاية متوالية الأعداد العقدية
نهاية متوالية الأعداد العقدية
![]() إذا أمكن إيجاد جوار لـ
إذا أمكن إيجاد جوار لـ![]() يحوي
جميع نقاط المتوالية ماعدا عدداً منتهياً منها ونكتب:
يحوي
جميع نقاط المتوالية ماعدا عدداً منتهياً منها ونكتب:
![]()
تكون المجموعة ![]() مجموعة متصلة إذا كان من
الممكن أن نصل ما بين كل نقطتين منها بخط جميع نقاطه منتمية لـ
مجموعة متصلة إذا كان من
الممكن أن نصل ما بين كل نقطتين منها بخط جميع نقاطه منتمية لـ
![]() .
.
المنطقة المفتوحة (الساحة) هي مجموعة مفتوحة متصلة.
المنطقة المغلقة هي مجموعة مغلقة متصلة.
مثلاً، المنطقة ![]() منطقة مفتوحة، بينما
منطقة مفتوحة، بينما
![]() منطقة مغلقة.
منطقة مغلقة.
1-6-2
التابع العقديليكن لدينا مجموعة الأعداد العقدية ![]() متحولا عقديا من
متحولا عقديا من ![]() كل من قسماه الحقيقي والتخيلي متحولان ,
ولنفرض أنه من أجل أي قيمة لـ
كل من قسماه الحقيقي والتخيلي متحولان ,
ولنفرض أنه من أجل أي قيمة لـ![]() من المجموعة
من المجموعة
![]() أمكن تعيين عدد عقدي
أمكن تعيين عدد عقدي ![]() حيث أن:
حيث أن:
![]()
نقول أن ![]() تابع للمتحول
تابع للمتحول
![]() ، ويكون هذا التابع وحيد التعيين في المجموعة
، ويكون هذا التابع وحيد التعيين في المجموعة
![]() إذا كان من أجل كل قيمة
إذا كان من أجل كل قيمة ![]() يوجد
قيمة وحيدة للتابع
يوجد
قيمة وحيدة للتابع ![]() .
.
أي أنه إذا كان ![]() فان
فان
![]() وذلك من أجل
وذلك من أجل ![]()
مثال
:إذا كان: ![]()
فإن: ![]()
وبالتالي:
![]()
لذلك:
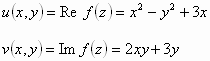
وفي النقطة ![]() للتابع
للتابع
![]() قيمة وحيدة هي:
قيمة وحيدة هي:
![]()
مثال
:التابع ![]()
ثنائي التعيين وذلك لأنه من أجل كل قيمة لـ
![]() يقابلها قيمتان للتابع
يقابلها قيمتان للتابع
![]() حيث أن:
حيث أن:
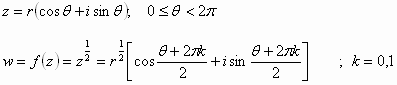
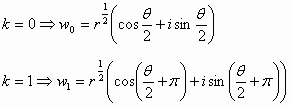
1-6-3
النهاياتنقول عن متتالية الأعداد العقدية ![]() بأنها
متقاربة للنهاية
بأنها
متقاربة للنهاية![]() ونكتب
ونكتب ![]() إذا كان
من أجل
إذا كان
من أجل ![]() عددا موجبا يوجد عدد موجب
عددا موجبا يوجد عدد موجب
![]() بحيث يكون:
بحيث يكون:
![]()
نهاية
تابع:نقول بالتعريف أن التابع ![]() ينتهي إلى
ينتهي إلى
![]() عندما
عندما ![]() ونكتب:
ونكتب:
![]()
إذا وفقط إذا كان من أجل ![]() يمكن إيجاد
العدد
يمكن إيجاد
العدد ![]() بحيث يكون
بحيث يكون ![]() من أجل جميع
قيم
من أجل جميع
قيم ![]() المحققة للمتراجحة
المحققة للمتراجحة ![]() .
.
مثال
:برهن أن: ![]()
البرهان:
![]()
ومنه ينتج أن : ![]() ، أي أن
، أي أن
![]() .
.