1-7
التوابع التحليليةتعريف:
يكون التابع ![]() تحليلياً (هولومورفي) في
النقطة
تحليلياً (هولومورفي) في
النقطة ![]() إذا كان التابع وحيد التعيين وقابلاً للاشتقاق في
النقطة
إذا كان التابع وحيد التعيين وقابلاً للاشتقاق في
النقطة ![]() وفي كل جوار لـ
وفي كل جوار لـ![]() .
.
تعريف:
يكون التابع ![]() تحليلياً في المنطقة
تحليلياً في المنطقة
![]() إذا كان تحليلياً في كل نقاط هذه المنطقة ما عدا عدد
محدود منها والتي تسمى بالنقاط الشاذة
إذا كان تحليلياً في كل نقاط هذه المنطقة ما عدا عدد
محدود منها والتي تسمى بالنقاط الشاذة
تعريف:
يكون التابع ![]() صحيحاً (منتظماً) إذا كان
تحليلياً في جميع نقاط المستوي العقدي وبما أن كل كثير حدود
صحيحاً (منتظماً) إذا كان
تحليلياً في جميع نقاط المستوي العقدي وبما أن كل كثير حدود
![]() قابلاً للاشتقاق في أية نقطة من المستوي العقدي ووحيد
التعيين أيضاً نستنتج أن كل كثير حدود:
قابلاً للاشتقاق في أية نقطة من المستوي العقدي ووحيد
التعيين أيضاً نستنتج أن كل كثير حدود:
![]()
هو تابع صحيح.
مثال
:إن التابع ![]() و مشتقه
و مشتقه
![]() هو تحليلي في أي نقطة ما عدا
هو تحليلي في أي نقطة ما عدا ![]() و هي نقطة شاذة.
و هي نقطة شاذة.
1-7-1
شروط كوشي وريمانليكن لدينا التابع العقدي التحليلي:
![]()
لنفرض أن التابع ![]() معرف ومستمر في جوار
نقطة ما
معرف ومستمر في جوار
نقطة ما ![]() وقابلاً للاشتقاق في هذه النقطة عندئذ من
التعريف نجد أن:
وقابلاً للاشتقاق في هذه النقطة عندئذ من
التعريف نجد أن:
![]()
ليكن ![]() .
.
لنختار الآن الطريق ![]() لنجعل
لنجعل
![]() أولاً ثم
أولاً ثم

![]() بوضع
بوضع ![]() نجد أن
نجد أن
![]() ومنه:
ومنه:
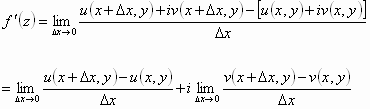
وحيث أن ![]() موجود فإن النهايتين موجودتين
أيضاً وهما المشتقات الجزئية لـ
موجود فإن النهايتين موجودتين
أيضاً وهما المشتقات الجزئية لـ![]() و
و
![]() بالنسبة لـ
بالنسبة لـ ![]() لذلك:
لذلك:
![]()
وبشكل مشابه، إذا أخذنا الطريق ![]() وبوضع
وبوضع
![]() أولاً فإن:
أولاً فإن:
![]()
![]()
أي أن:
![]()
وذلك لأن ![]() ، وبما أن
، وبما أن
![]() موجود بالفرض إذاً:
موجود بالفرض إذاً:
![]()
ومنه نجد أن ![]() و
و
![]() ، وهذه الشروط تسمى شروط كوشي وريمان، وبالتالي يمكن
الحصول على النظرية التالية:
، وهذه الشروط تسمى شروط كوشي وريمان، وبالتالي يمكن
الحصول على النظرية التالية:
نظرية:
لكي يكون التابع ![]() تحليلياً في المنطقة
تحليلياً في المنطقة
![]() يلزم ويكفي أن يكون
يلزم ويكفي أن يكون ![]() و
و![]() قابلين للاشتقاق الجزئي من المرتبة الأولى في كل نقطة من
قابلين للاشتقاق الجزئي من المرتبة الأولى في كل نقطة من ![]() ومحققين لشروط كوشي وريمان.
ومحققين لشروط كوشي وريمان.
البرهان:
لزوم الشرط:
لنفرض أن التابع ![]() تحليلي ولنبرهن أنه
يحقق شروط كوشي وريمان بأن التابع
تحليلي ولنبرهن أنه
يحقق شروط كوشي وريمان بأن التابع ![]() تحليلي، بما أن
المشتقات الجزئية الأولى لـ
تحليلي، بما أن
المشتقات الجزئية الأولى لـ ![]() و
و ![]() مستمرة في المنطقة
مستمرة في المنطقة ![]() فإنه يمكن أن نكتب:
فإنه يمكن أن نكتب:
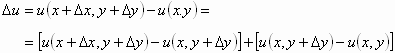
![]()
حيث أن ![]() و عندما
و عندما
![]() ، وبشكل مشابه نجد أن:
، وبشكل مشابه نجد أن:
![]()
لنحسب الآن ![]() :
:
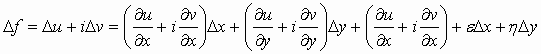
![]()
وبتطبيق شروط كوشي ريمان نجد أن:
![]()
ولكن:
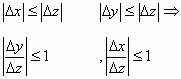
وبتقسيم طرفي العلاقة على ![]() ، وعندما
، وعندما![]() نحصل على:
نحصل على:
![]()
ولها نهاية وحيدة في النقطة ![]() والتابع
والتابع
![]() تحليلي في المنطقة
تحليلي في المنطقة ![]() .
.
وإذا كان التابع ![]() تحليلياً في المنطقة
تحليلياً في المنطقة
![]() من أجل أي نقطة
من أجل أي نقطة ![]() فإن:
فإن:
![]()