أمثلة
محلولة:مثال
:مثل هندسياً مجموعة قيم
![]() التي تحقق العلاقة
التي تحقق العلاقة
![]()
الحل :
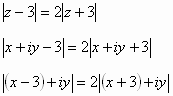
ومنه:
![]()
بتربيع الطرفين نجد:
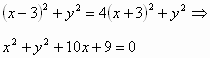
وهي معادلة دائرة مركزها ![]() ونصف قطرها
ونصف قطرها![]() ، حيث أن المعادلة تكتب بالشكل
، حيث أن المعادلة تكتب بالشكل![]() .
.
مثال
:بين فيما إذا كان التابع:
![]()
قابلاً للاشتقاق وعين قيم ![]() التي لا يكون
من أجلها مستمراً.
التي لا يكون
من أجلها مستمراً.
الحل:
![]()

ونلاحظ أن:
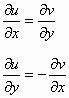
والتابع تحليلي من أجل جميع قيم![]() ما عدا
ما عدا
![]() ، وقابل للاشتقاق ما عدا
، وقابل للاشتقاق ما عدا ![]()
ونلاحظ أنه يمكن كتابة المخرج بالشكل:
![]()
وبالتالي:
![]()
وهذا التابع غير مستمر من أجل ![]() ، والتابع
تحليلي من أجل جميع قيم
، والتابع
تحليلي من أجل جميع قيم ![]() ما عدا
ما عدا ![]() ، والتابع قابل للاشتقاق ما عدا
، والتابع قابل للاشتقاق ما عدا ![]() ، ونلاحظ أنه يمكن كتابة
المخرج بالشكل:
، ونلاحظ أنه يمكن كتابة
المخرج بالشكل:
![]()
وبالتالي :
![]()
وهذا التابع غير مستمر من أجل ![]()
مثال
:أثبت أن التابع ![]() تحليلي.
تحليلي.
الحل:
إن الشرط القطبي شرطي كوشي وريمان هو:
![]()
ومنه:
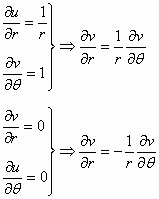
والتابع ![]() تحليلي
تحليلي
مثال
:برهن أن التابع ![]() ، توافقي ثم احسب التابع
المرافق
، توافقي ثم احسب التابع
المرافق ![]() الذي يجعل التابع
الذي يجعل التابع ![]() تحليلي.
تحليلي.
الحل:
لكي يكون التابع ![]() توافقي يجب أن يحقق
معادلة لابلاس:
توافقي يجب أن يحقق
معادلة لابلاس:
![]()
![]()
![]()
ومنه:
![]()
وبما أن معادلة لابلاس محققة إذا التابع u توافقي ، لحساب التابع v نستخدم معادلات كوشي ريمان:
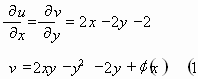
ومن معادلة كوشي ريمان الثانية نجد ![]() :
:
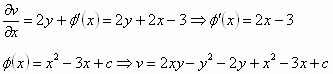
مثال
:برهن أن مجموع جذور المعادلة:
![]()
هو ![]() وأن جداء الجذور هو
وأن جداء الجذور هو
![]()
الحل:
المعادلة يمكن أن تكتب بالشكل:
![]()
حيث أن ![]() تمثل جذور المعادلة.
تمثل جذور المعادلة.
المعادلة السابقة تكتب بالشكل:
![]()
ومنه :
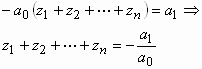
وكذلك:
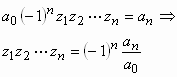
مثال
:إذا كان ![]() برهن أن:
برهن أن:
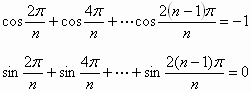
الحل:
لنأخذ المعادلة :
![]()
والتي حلولها تمثل الجذر النوني للعدد واحد.
![]()
مجموع هذه الحلول يساوي الصفر أي أن:
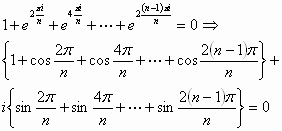
بالمطابقة نحصل على الحل.