أوجد كل مما يلي:

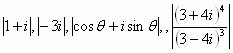
أوجد قيمة

لكل من التوابع التالية

أوجد القسم الحقيقي والتخيلي للتوابع التالية:

أوجد مشتق كلا من التوابع التالية في النقطة

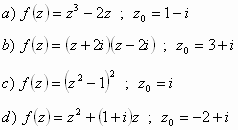
إذا كانت معادلات كوشي ريمان في الشكل القطبي تكتب بالشكل:

حيث أن ، برهن أن معادلات لابلاس في الإحداثيات القطبية هي:

ليكن ، برهن أن هذا التابع تحليلي

أي من التوابع التالية تحليلي

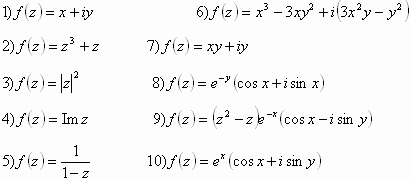
برهن أن التوابع التالية توافقية ثم أوجد التوابع التحليلية المرافقة لها:

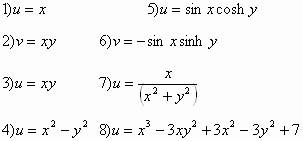
تحت أي شرط تكون التوابع التالية توافقية:

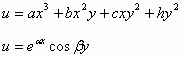
إذا كان تابع تحليلي في المنطقة و ثابت في هذا المجال برهن أن التابع تابع ثابت.

برهن أن :

إذا كان :

فإن:

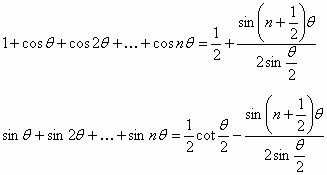
13. برهن أنه من أجل فإن :